Difference between revisions of "RotorcraftMixing"
| (19 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
[[Image:hexa_3D.png]] | This page describe how to compute "mixing" for an arbitrary multirotors configuration. | ||
[[Image:hexa_3D.png|800px]] | |||
== Introduction == | |||
"Mixing" consist in converting rotational accelerations commands computed by the autopilot into throttle commands for each of the motor controllers. | |||
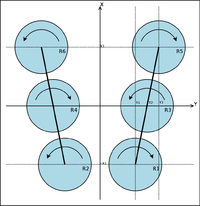
Let us consider a vehicle comprising a set of <math>N</math> identical fixed pitch rotors <math>R_i, i \in[1:N]</math> located at coordinates <math>(X_i,Y_i, 0), i\in[1:N]</math> and spinning in the same plane in the direction <math>D_i, i\in[1:N], D_i\in[-1;1]</math> at a rotational speed <math>\omega_i, i\in[1:N]</math>. | |||
Assuming a quasi hovering regime, the force produced by each rotor can be considered normal to the rotor plane and proportional to the square of its rotational speed. Expressed in body frame ( front, right, down ), this leads to | |||
<math> | |||
\overrightarrow{F}_{i}^{B} = \begin{pmatrix}0\\0\\-C_t \omega_i^2\end{pmatrix} | |||
</math> | |||
Under the same assumption, the torque produced by each rotor can also be assumed to be in the same direction and proportional to the square of the rotational speed. | |||
The torque produced by each rotor around the CG, expressed in body frame can then be writen | |||
<math> | |||
\overrightarrow{M}_{i}^{B} = \begin{pmatrix}X_i\\Y_i\\0\end{pmatrix}\wedge\begin{pmatrix}0\\0\\-C_t \omega_i^2\end{pmatrix} + \begin{pmatrix}0\\0\\D_i C_m \omega_i^2\end{pmatrix} | |||
</math> | |||
<math> | |||
\overrightarrow{M}_{i}^{B} = C_t \omega_i^2 \begin{pmatrix}-Y_i \\X_i \\D_i \frac{C_m}{C_t}\end{pmatrix} | |||
</math> | |||
Where <math>C_t</math> is a "thrust" coefficient and <math>Cm</math> is a "torque" coefficient. It has been measured experimentally that <math>\frac{Ct}{Cm} \approx 10</math> on a mikrokopter. | |||
As a first approximation we can consider that the rotational speed of the propeller is proportional to the square root of the applied command <math>u_i</math> | |||
<math> | |||
\omega_i^2 = K u_i | |||
</math> | |||
This allows us to express the torque produced by the set of rotors as | |||
<math> | |||
\overrightarrow{M}^{B} = \sum_{i=1}^{N} \overrightarrow{M}_{i}^{B} = K C_t | |||
\begin{pmatrix} | |||
-\sum_{i=1}^{N} Y_i u_i\\ | |||
\sum_{i=1}^{N} X_i u_i\\ | |||
\frac{C_m}{C_t} \sum_{i=1}^{N} D_i u_i | |||
\end{pmatrix} | |||
</math> | |||
which can be rewriten as a matrix vector product | |||
<math> | |||
\overrightarrow{M}^{B} = | |||
K C_t | |||
\begin{pmatrix} | |||
-Y_1&-Y_2&\ldots&-Y_n\\ | |||
X_1& X_2&\ldots& X_n\\ | |||
\frac{C_m}{Ct}D_1&\frac{C_m}{Ct}D_2&\ldots&\frac{C_m}{Ct}D_n | |||
\end{pmatrix} | |||
\begin{pmatrix} | |||
u_1\\ | |||
u_2\\ | |||
\vdots\\ | |||
u_n | |||
\end{pmatrix} | |||
</math> | |||
<math> | |||
\overrightarrow{M}^{B} = A \overrightarrow{U} | |||
</math> | |||
<math>A</math> is a <math>3*N</math> matrix describing the geometric positions of our rotors and <math>U</math> is the vector of throttle commands for our set of motor controllers. | |||
In order to express the command applied to each power train as a function of the momentum we want to apply to our vehicle, we need to find <math>B</math>, a <math>N*3</math> matrix such as | |||
<math> | |||
\overrightarrow{U} = B \overrightarrow{M}^B | |||
</math> | |||
If <math>A</math> has rank 3, we know that such a matrix exists (yeah, we can't do 2 rotors or have all rotors aligned), and in this case, we have the relationship | |||
<math> | |||
AB = \mathcal{I}_3 | |||
</math> | |||
We know that one solution of this equation is the Moore-Penrose pseudoinverse of <math>A</math>. | |||
Furthermore, this solution is the one leading to the power train command vector having the smallest euclidian norm, which is interesting as it optimizes the repartion of our control effort across our power trains. | |||
== Example == | |||
Let's consider the following H hexarotors configuration. | |||
[[Image:hexa_h.png|200px]] | |||
<math> | |||
A = | |||
\begin{pmatrix} | |||
-0.17 & 0.17 &-0.25& 0.25&-0.33 & 0.33 \\ | |||
-0.35 &-0.35 & 0 & 0 & 0.35 & 0.35 \\ | |||
-0.1 & 0.1 & 0.1 &-0.1 &-0.1 & 0.1 | |||
\end{pmatrix} | |||
</math> | |||
The first two lines of the <math>A</math> matrix represent the coordinates of each rotor in the <math>X,Y</math> plane, and the third line the direction in which they spin. Note that in this example the X axis is vertical, and the Y coordinates are in the top row of <math>A</math>. | |||
<math> | |||
B = | |||
\begin{pmatrix} | |||
-0.24 & -0.71 & -1.47 \\ | |||
0.241 & -0.71 & 1.47 \\ | |||
-0.93 & 0. & 2.44 \\ | |||
0.93 & 0. & -2.44 \\ | |||
-0.69 & 0.71 & -1.09 \\ | |||
0.69 & 0.71 & 1.09 | |||
\end{pmatrix} | |||
</math> | |||
Normalizing columns of <math>B</math> yelds | |||
<math> | |||
\tilde{B} = | |||
\begin{pmatrix} | |||
-67 & -256 & -154 \\ | |||
67 & -256 & 154 \\ | |||
-256 & 0 & 256 \\ | |||
256 & 0 & -256 \\ | |||
-189 & 256 & -115 \\ | |||
189 & 256 & 115 \\ | |||
\end{pmatrix} | |||
</math> | |||
which in turns yelds the following supervision section | |||
<pre> | |||
<section name="MIXING" prefix="MOTOR_MIXING_"> | |||
<define name="TRIM_ROLL" value="0"/> | |||
<define name="TRIM_PITCH" value="0"/> | |||
<define name="TRIM_YAW" value="0"/> | |||
<define name="NB_MOTOR" value="6"/> | |||
<define name="SCALE" value="256"/> | |||
<define name="ROLL_COEF" value="{ -67, 67, -256, 256, -189, 189}"/> | |||
<define name="PITCH_COEF" value="{ -256, -256, 0, 0, 256, 256}"/> | |||
<define name="YAW_COEF" value="{ -154, 154, 256, -256, -115, 115}"/> | |||
<define name="THRUST_COEF" value="{ 256, 256, 256, 256, 256, 256}"/> | |||
</section> | |||
</pre> | |||
== IPython/Numpy == | |||
'''The [https://github.com/paparazzi/paparazzi/blob/master/sw/tools/motor_mixing.py sw/tools/motor_mixing.py] script in paparazzi can be used to calculate and print configurations.''' | |||
The above computation can be performed in a simple python script with numpy (or interactively using ipython). [http://nbviewer.ipython.org/6909831 example RotorcraftMixing.ipynb in IPython notebook viewer] | |||
<source lang="python"> | |||
import numpy as np | |||
A = np.array([[-0.17, 0.17, -0.25, 0.25, -0.33, 0.33], | |||
[-0.35, -0.35, 0., 0., 0.35, 0.35], | |||
[-0.1, 0.1, 0.1, -0.1, -0.1, 0.1 ]]) | |||
# Moore-Penrose pseudoinverse of A | |||
B = np.linalg.pinv(A) | |||
# normalizing columns of B and transpose | |||
B_normalized = (B.T / B.max(axis=0)[:, np.newaxis]) | |||
# scale and round to 256 to return final coefficients | |||
coeffs = np.around(256 * B_normalized).astype(int) | |||
# nicely output result as defines for copy-pasting | |||
import string | |||
rows = ['ROLL_COEF" ', 'PITCH_COEF" ', 'YAW_COEF" '] | |||
for i, r in enumerate(rows): | |||
print('<define name="' + r + 'value="{' + string.join(['{:>4d}'.format(c) for c in coeffs[i]], ', ') + '}"/>') | |||
</source> | |||
resulting in the output: | |||
<pre> | |||
<define name="ROLL_COEF" value="{ -67, 67, -256, 256, -189, 189}"/> | |||
<define name="PITCH_COEF" value="{-256, -256, 0, 0, 256, 256}"/> | |||
<define name="YAW_COEF" value="{-154, 154, 256, -256, -115, 115}"/> | |||
</pre> | |||
== Octave == | |||
The above computation can be performed using the following simple octave script (sudo apt-get install octave3.2) | |||
octave | |||
copy the flowing commands in the terminal: (ncol is the number of col from matrix B. in this example = 3 ) | |||
exit | |||
<pre> | |||
A = [ | |||
-0.17 0.17 -0.25 0.25 -0.33 0.33 | |||
-0.35 -0.35 0. 0. 0.35 0.35 | |||
-0.1 0.1 0.1 -0.1 -0.1 0.1 | |||
]; | |||
B = pinv(A) | |||
m = max(abs(B)) | |||
[nrow,ncol] = size(B) | |||
for i=1:ncol | |||
Btilde(:,i) = B(:,i)/m(i); | |||
end | |||
Btilde = round(256*Btilde) | |||
</pre> | |||
[[Category:Software]] [[Category:User_Documentation]] | |||
Latest revision as of 14:09, 9 July 2015
This page describe how to compute "mixing" for an arbitrary multirotors configuration.
Introduction
"Mixing" consist in converting rotational accelerations commands computed by the autopilot into throttle commands for each of the motor controllers.
Let us consider a vehicle comprising a set of identical fixed pitch rotors located at coordinates and spinning in the same plane in the direction at a rotational speed .
Assuming a quasi hovering regime, the force produced by each rotor can be considered normal to the rotor plane and proportional to the square of its rotational speed. Expressed in body frame ( front, right, down ), this leads to
Under the same assumption, the torque produced by each rotor can also be assumed to be in the same direction and proportional to the square of the rotational speed.
The torque produced by each rotor around the CG, expressed in body frame can then be writen
Where is a "thrust" coefficient and is a "torque" coefficient. It has been measured experimentally that on a mikrokopter.
As a first approximation we can consider that the rotational speed of the propeller is proportional to the square root of the applied command
This allows us to express the torque produced by the set of rotors as
which can be rewriten as a matrix vector product
is a matrix describing the geometric positions of our rotors and is the vector of throttle commands for our set of motor controllers.
In order to express the command applied to each power train as a function of the momentum we want to apply to our vehicle, we need to find , a matrix such as
If has rank 3, we know that such a matrix exists (yeah, we can't do 2 rotors or have all rotors aligned), and in this case, we have the relationship
We know that one solution of this equation is the Moore-Penrose pseudoinverse of . Furthermore, this solution is the one leading to the power train command vector having the smallest euclidian norm, which is interesting as it optimizes the repartion of our control effort across our power trains.
Example
Let's consider the following H hexarotors configuration.
The first two lines of the matrix represent the coordinates of each rotor in the plane, and the third line the direction in which they spin. Note that in this example the X axis is vertical, and the Y coordinates are in the top row of .
Normalizing columns of yelds
which in turns yelds the following supervision section
<section name="MIXING" prefix="MOTOR_MIXING_">
<define name="TRIM_ROLL" value="0"/>
<define name="TRIM_PITCH" value="0"/>
<define name="TRIM_YAW" value="0"/>
<define name="NB_MOTOR" value="6"/>
<define name="SCALE" value="256"/>
<define name="ROLL_COEF" value="{ -67, 67, -256, 256, -189, 189}"/>
<define name="PITCH_COEF" value="{ -256, -256, 0, 0, 256, 256}"/>
<define name="YAW_COEF" value="{ -154, 154, 256, -256, -115, 115}"/>
<define name="THRUST_COEF" value="{ 256, 256, 256, 256, 256, 256}"/>
</section>
IPython/Numpy
The sw/tools/motor_mixing.py script in paparazzi can be used to calculate and print configurations.
The above computation can be performed in a simple python script with numpy (or interactively using ipython). example RotorcraftMixing.ipynb in IPython notebook viewer
import numpy as np
A = np.array([[-0.17, 0.17, -0.25, 0.25, -0.33, 0.33],
[-0.35, -0.35, 0., 0., 0.35, 0.35],
[-0.1, 0.1, 0.1, -0.1, -0.1, 0.1 ]])
# Moore-Penrose pseudoinverse of A
B = np.linalg.pinv(A)
# normalizing columns of B and transpose
B_normalized = (B.T / B.max(axis=0)[:, np.newaxis])
# scale and round to 256 to return final coefficients
coeffs = np.around(256 * B_normalized).astype(int)
# nicely output result as defines for copy-pasting
import string
rows = ['ROLL_COEF" ', 'PITCH_COEF" ', 'YAW_COEF" ']
for i, r in enumerate(rows):
print('<define name="' + r + 'value="{' + string.join(['{:>4d}'.format(c) for c in coeffs[i]], ', ') + '}"/>')
resulting in the output:
<define name="ROLL_COEF" value="{ -67, 67, -256, 256, -189, 189}"/>
<define name="PITCH_COEF" value="{-256, -256, 0, 0, 256, 256}"/>
<define name="YAW_COEF" value="{-154, 154, 256, -256, -115, 115}"/>
Octave
The above computation can be performed using the following simple octave script (sudo apt-get install octave3.2)
octave copy the flowing commands in the terminal: (ncol is the number of col from matrix B. in this example = 3 ) exit
A = [ -0.17 0.17 -0.25 0.25 -0.33 0.33 -0.35 -0.35 0. 0. 0.35 0.35 -0.1 0.1 0.1 -0.1 -0.1 0.1 ]; B = pinv(A) m = max(abs(B)) [nrow,ncol] = size(B) for i=1:ncol Btilde(:,i) = B(:,i)/m(i); end Btilde = round(256*Btilde)


![{\displaystyle R_{i},i\in [1:N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24e6e2262c991080b430d6d3964e43e2a3e7711f)
![{\displaystyle (X_{i},Y_{i},0),i\in [1:N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a45f0e29a626151876388cad6f2b0fe1a17c48d)
![{\displaystyle D_{i},i\in [1:N],D_{i}\in [-1;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23e0ca0cec389eccdbf2b16d5ddb49b14b1717ce)
![{\displaystyle \omega _{i},i\in [1:N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbed16b40bf77b2d4d6928edd0b3c4d01f202a1e)