ControlTheory

Dynamic Systems

• Notion of State

 The state of a dynamic system represents the minimal quantity of information required in order to be able to predict its future,
knowing its equation of dynamic and its inputs.

You can think of the state of a system as the frontier between past and future : two systems of identical dynamic and identical state will have the same trajectory in the future when applied the same inputs, whatever their past can be.

• State Space Representation

State Estimation

In order to be able to control a vehicle, ie to steer it along a trajectory, a first prerequisite is to know its state. Typically, sensors are used to obtain this information. Sadly, sensors won't give you a straightforward knowledge of the state of the vehicle. The information is likely to be partial ( we have an altitude sensor, but nothing to measure vertical speed) and will also likely contain "errors" (bias, noise, latency, etc... ). You can always get more sensors and/or better sensors, but there's no such thing as a perfect sensor. The process of reconstructing the state of a dynamic system using a number of incomplete and erroneous measurements is called state estimation or state observation.

Let's start with an example :

We are interested in controlling the altitude of a vehicle. We measure this altitude using for example a barometer. As we will see later, the vertical speed of the vehicle is a mandatory information in order to be able to achieve a satisfactory control. So, how do we obtain the vertical speed information ?

• Direct Differentiation

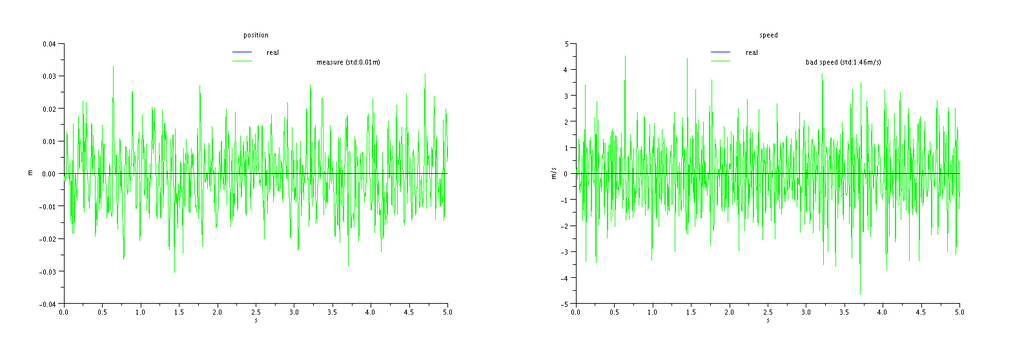
A first idea would be to take the difference between two consecutive altitude measurements and divide that quantity by the duration between the two measurements. This is indeed a bad idea. Let's see one of the reasons why.

Our barometer being a real world instrument, it will output noisy measurements ( think electrical noise, etc...). Let's use a little simulation to see what happens when you differentiate noisy measurements:

The noise gets amplified by the division by the sampling interval ( and we did not even introduce inaccuracy in that sampling interval ). In the above simulation, starting with a very good sensor having 1cm noise standard deviation and sampling at 100Hz, we obtain an estimate for the vertical speed having 1.4m/s of standard deviation. Pretty unusable...

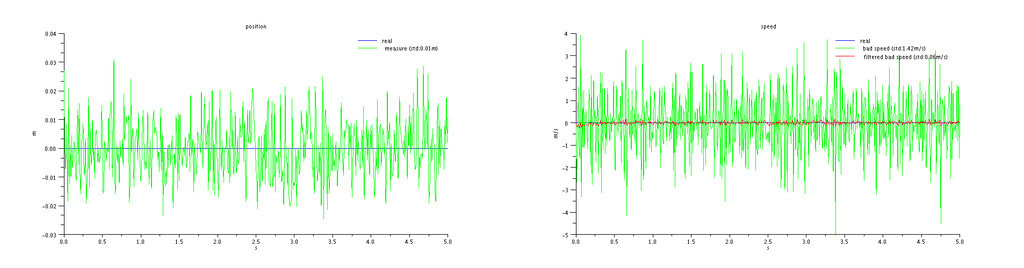
• Let's filter that noise out

A second idea would be to attempt and filter that noise. Let's run for example our estimate through a first order low pass filter. Here is the result of the simulation

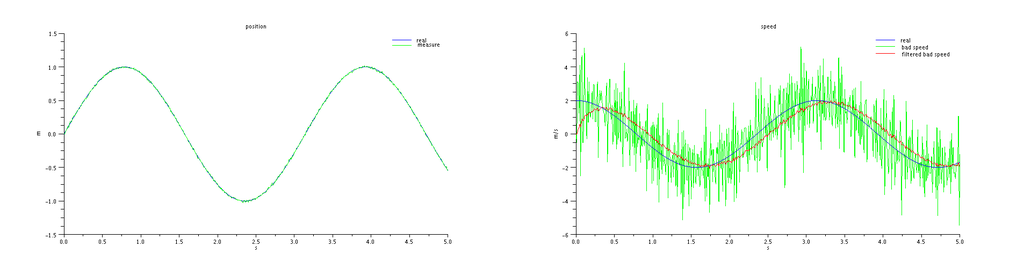
Yay ! We reduced noise on our vertical speed estimate to 6cm/s. Did we achieve something interesting when doing so ? sadly no. As shown on the next plot where we have run the same algorithm on a moving vehicle, we have introduced lag in our estimate.

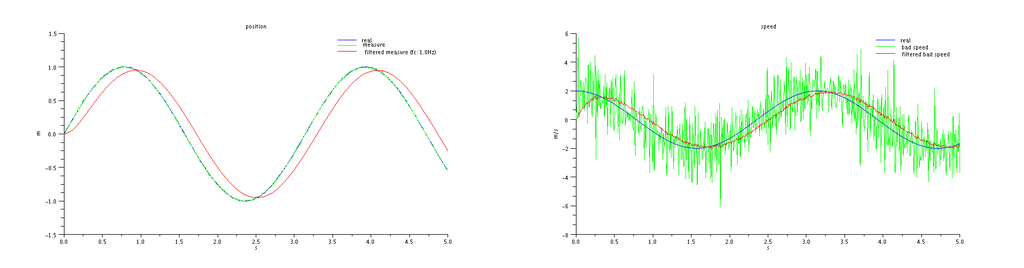
And lag is bad for control as we'll show later. What would have happened if we had filtered the measurement before differentiating ? same punishment, as shown in the next plot produced by the following simulation...

so, is there a better way ?

• Let's introduce Kinematics

$X={\begin{pmatrix}z\\{\dot {z}}\end{pmatrix}}$

${\dot {X}}(t)={\begin{pmatrix}0&1\\0&0\end{pmatrix}}X(t)+{\begin{pmatrix}0\\1\end{pmatrix}}a(t)$

We don't really have an idea of the acceleration of our system, so let's asume it's 0 for now. When using this hypothesis and switching to discrete time (more on this later), we obtain the following equation:

$X_{t+dt}={\begin{pmatrix}1&dt\\0&1\end{pmatrix}}X_{t}$

--Poine 14:43, 13 November 2009 (CET)