Difference between revisions of "User:Jouvencel"
| Line 61: | Line 61: | ||
- <math>q_e = 1</math> | - <math>q_e = 1</math> | ||
- <math>q_x = \psi/2 - \theta/2 \phi/2 = \psi/2 </math> | - <math>q_x = \psi/2 - \theta/2 * \phi/2 = \psi/2 </math> | ||
- <math>q_y = \theta/2 - \psi/2 \phi/2 = \theta/2 </math> | - <math>q_y = \theta/2 - \psi/2 *\phi/2 = \theta/2 </math> | ||
- <math>q_z = \phi/2 - \theta/2 \psi/2 = \phi/2 </math> | - <math>q_z = \phi/2 - \theta/2 * \psi/2 = \phi/2 </math> | ||
Revision as of 03:09, 6 August 2013
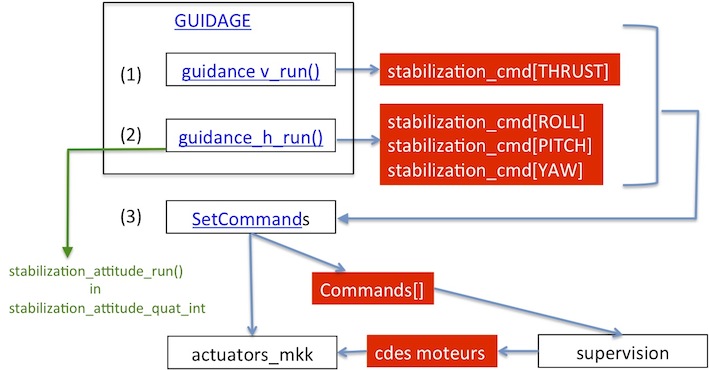
Control command based of quaternions
Files : stabilization_attitude_quat_int.c (.h)
stabilization_attitude_ref_quat_int.c (.h)
quat_setpoint_int.c (.h)
- Position in the autopilot structure
- Control structure
note : () number of decimals for integer calculus
- Comments
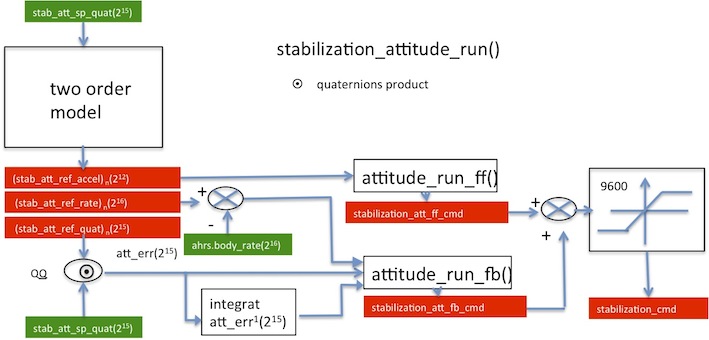
- "stab_att_sp_quat (15)" attitude to reach
- "stab_att_ref_accel(12)", "stab_att_ref_rate(16)","stab_att_ref_quat(15)" references défined by two order model
- stabilization_cmd[X] (X=ROLL, PITCH, YAW) commands défined by a feedforward part and feedback part, feedback part is based on PID
- quaternions define the orientation of rotorcraft,
- the error between the quat_sp and the quat_ref is computed by a quaternion product,
- the dot_quaternion is computed by the formula
- The second order model :
-- Computes integrated accelerate to obtain "stab_att_ref_rate" by the Euler method
-- Computes integrated rate to obtain "stab_att_ref_quat" by the Euler method
-- The Euler method uses dt here, dt is implicite and equal 1/512 or ,
-- Determines the stab_att_ref_accel(12) by a second order with and . and are defined in airframe.xml.
- The second order
- Feedforward part
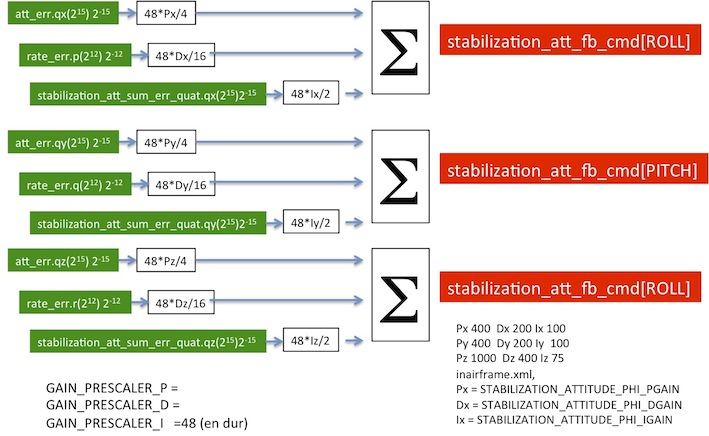
- Feedback part
- Comments
With the assumption of small variations so and so on for pitch and yaw, terms of second order are ignored :
-
-
-
-