Difference between revisions of "ControlTheory"
| Line 4: | Line 4: | ||
In order to be able to control a vehicle, ie to steer it along a trajectory, a first prerequisite is to know its state. | In order to be able to control a vehicle, ie to steer it along a trajectory, a first prerequisite is to know its state. | ||
Typically, sensors are used to obtain this information. Sadly, sensors won't give you a straightforward knowledge of the state of the vehicle. The information is likely to be partial ( we have an altitude sensor, but nothing to measure vertical speed) and will also likely contain "errors" (bias, noise, latency, etc... ). You can always get more sensors or better sensors, but there's no such thing as a perfect sensor. The process of reconstructing the state of a dynamic system using a number of incomplete and erroneous measurements is called ''state estimation'' or ''state observation''. | Typically, sensors are used to obtain this information. Sadly, sensors won't give you a straightforward knowledge of the state of the vehicle. The information is likely to be partial ( we have an altitude sensor, but nothing to measure vertical speed) and will also likely contain "errors" (bias, noise, latency, etc... ). You can always get more sensors and/or better sensors, but there's no such thing as a perfect sensor. The process of reconstructing the state of a dynamic system using a number of incomplete and erroneous measurements is called ''state estimation'' or ''state observation''. | ||
Let's start with an example : | Let's start with an example : | ||
| Line 10: | Line 10: | ||
We are interested in controlling the altitude of a vehicle. We measure this altitude using for example a barometer. As we will see later, the vertical speed of the vehicle is a mandatory information in order to be able to achieve a satisfactory control. So, how do we obtain the vertical speed information ? | We are interested in controlling the altitude of a vehicle. We measure this altitude using for example a barometer. As we will see later, the vertical speed of the vehicle is a mandatory information in order to be able to achieve a satisfactory control. So, how do we obtain the vertical speed information ? | ||
* Direct Differentiation | |||
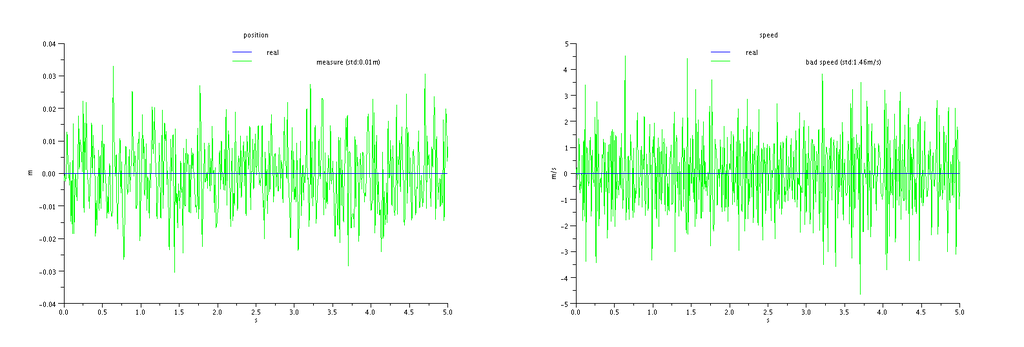
A first idea would be to take the difference between two consecutive altitude measurements and divide that quantity by the time between the two measurements. This is indeed a bad idea. Let's see one of the reasons why. | A first idea would be to take the difference between two consecutive altitude measurements and divide that quantity by the time between the two measurements. This is indeed a bad idea. Let's see one of the reasons why. | ||
| Line 19: | Line 20: | ||
The noise gets amplified by the division by the sampling interval ( and we did not even introduce inaccuracy in that sampling interval ). | The noise gets amplified by the division by the sampling interval ( and we did not even introduce inaccuracy in that sampling interval ). | ||
In the above simulation, starting with a very good sensor having 1cm noise standard deviation, we obtain an estimate for the vertical speed having 1.4m of standard deviation. Pretty unusable... | In the above simulation, starting with a very good sensor having 1cm noise standard deviation, we obtain an estimate for the vertical speed having 1.4m of standard deviation. Pretty unusable... | ||
--[[User:Poine|Poine]] 14:43, 13 November 2009 (CET) | |||
Revision as of 06:43, 13 November 2009
Dynamic Systems
State Estimation
In order to be able to control a vehicle, ie to steer it along a trajectory, a first prerequisite is to know its state. Typically, sensors are used to obtain this information. Sadly, sensors won't give you a straightforward knowledge of the state of the vehicle. The information is likely to be partial ( we have an altitude sensor, but nothing to measure vertical speed) and will also likely contain "errors" (bias, noise, latency, etc... ). You can always get more sensors and/or better sensors, but there's no such thing as a perfect sensor. The process of reconstructing the state of a dynamic system using a number of incomplete and erroneous measurements is called state estimation or state observation.
Let's start with an example :
We are interested in controlling the altitude of a vehicle. We measure this altitude using for example a barometer. As we will see later, the vertical speed of the vehicle is a mandatory information in order to be able to achieve a satisfactory control. So, how do we obtain the vertical speed information ?
- Direct Differentiation
A first idea would be to take the difference between two consecutive altitude measurements and divide that quantity by the time between the two measurements. This is indeed a bad idea. Let's see one of the reasons why.
Our barometer being a real world instrument, it will give us noisy measurements ( think electrical noise, etc...). Let's use a little simulation to see what happens when you differentiate noisy measurements:
The noise gets amplified by the division by the sampling interval ( and we did not even introduce inaccuracy in that sampling interval ). In the above simulation, starting with a very good sensor having 1cm noise standard deviation, we obtain an estimate for the vertical speed having 1.4m of standard deviation. Pretty unusable...
--Poine 14:43, 13 November 2009 (CET)