Difference between revisions of "User:Jouvencel"
(Created page with "== Control command based of quaternions == Files : stabilization_attitude_quat_int.c (.h) stabilization_attitude_ref_quat_int.c (.h) quat_setpoint_int.c (.h) * Position in the …") |
|||
| Line 3: | Line 3: | ||
Files : | Files : | ||
stabilization_attitude_quat_int.c (.h) | stabilization_attitude_quat_int.c (.h) | ||
stabilization_attitude_ref_quat_int.c (.h) | stabilization_attitude_ref_quat_int.c (.h) | ||
quat_setpoint_int.c (.h) | quat_setpoint_int.c (.h) | ||
| Line 13: | Line 15: | ||
[[File:fiche2.jpg]] | [[File:fiche2.jpg]] | ||
note : (<math>2^ | note : (<math>2^{''N''}</math>) number of decimals for integer calculus | ||
* Comments | |||
- "stab_att_sp_quat (15)" attitude to reach | |||
- "stab_att_ref_accel(12)", "stab_att_ref_rate(16)","stab_att_ref_quat(15)" references défined by two order model | |||
- stabilization_cmd[X] (X=ROLL, PITCH, YAW) commands défined by a feedforward part and feedback part, feedback part is based on PID | |||
- quaternions define the orientation of rotorcraft, | |||
- the error between the quat_sp and the quat_ref is computed by a quaternion product, | |||
- the dot_quaternion is computed by the formula <math>\frac{1}{2} M_s(p,q,r) Q</math> | |||
- The second order model : | |||
-- Computes integrated accelerate to obtain "stab_att_ref_rate" by the Euler method | |||
-- Computes integrated rate to obtain "stab_att_ref_quat" by the Euler method | |||
-- The Euler method uses dt here, dt is implicite and equal 1/512 or <math>2^9</math>, | |||
-- Determines the stab_att_ref_accel(12) by a second order <math>\frac{\Omega^2}{s^2+2 \Zeta \Omega s + \Omega^2}</math> with <math>\Omega = 200*\pi/180</math> and <math>\Zeta = 0.9</math>.<math>\Omega </math> and <math>\Zeta </math> are defined in airframe.xml. | |||
* The second order | |||
[[File:fiche3.jpg]] | |||
Revision as of 02:50, 6 August 2013
Control command based of quaternions
Files : stabilization_attitude_quat_int.c (.h)
stabilization_attitude_ref_quat_int.c (.h)
quat_setpoint_int.c (.h)
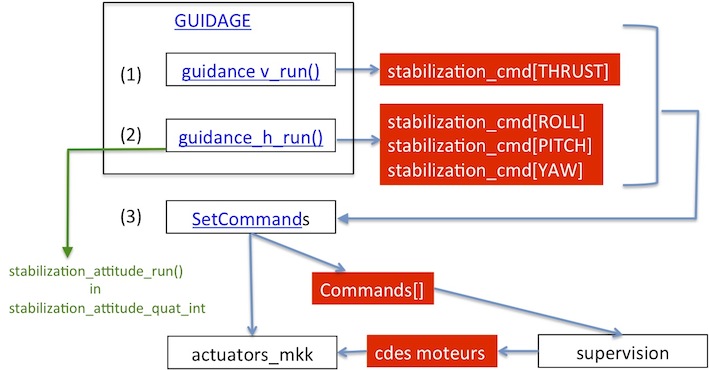
- Position in the autopilot structure
- Control structure
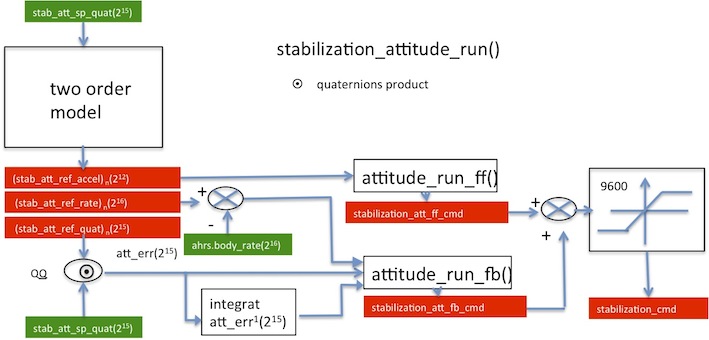
note : () number of decimals for integer calculus
- Comments
- "stab_att_sp_quat (15)" attitude to reach
- "stab_att_ref_accel(12)", "stab_att_ref_rate(16)","stab_att_ref_quat(15)" references défined by two order model
- stabilization_cmd[X] (X=ROLL, PITCH, YAW) commands défined by a feedforward part and feedback part, feedback part is based on PID
- quaternions define the orientation of rotorcraft,
- the error between the quat_sp and the quat_ref is computed by a quaternion product,
- the dot_quaternion is computed by the formula
- The second order model :
-- Computes integrated accelerate to obtain "stab_att_ref_rate" by the Euler method
-- Computes integrated rate to obtain "stab_att_ref_quat" by the Euler method
-- The Euler method uses dt here, dt is implicite and equal 1/512 or ,
-- Determines the stab_att_ref_accel(12) by a second order with and . and are defined in airframe.xml.
- The second order