Difference between revisions of "User:Jouvencel"
(Created page with "== Control command based of quaternions == Files : stabilization_attitude_quat_int.c (.h) stabilization_attitude_ref_quat_int.c (.h) quat_setpoint_int.c (.h) * Position in the …") |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
Files : | Files : | ||
stabilization_attitude_quat_int.c (.h) | |||
stabilization_attitude_ref_quat_int.c (.h) | - stabilization_attitude_quat_int.c (.h) | ||
quat_setpoint_int.c (.h) | |||
- stabilization_attitude_ref_quat_int.c (.h) | |||
- quat_setpoint_int.c (.h) | |||
* Position in the autopilot structure | * Position in the autopilot structure | ||
| Line 13: | Line 16: | ||
[[File:fiche2.jpg]] | [[File:fiche2.jpg]] | ||
note : (<math>2^ | note : (<math>2^{''N''}</math>) number of decimals for integer calculus | ||
* Comments | |||
- "stab_att_sp_quat (15)" attitude to reach | |||
- "stab_att_ref_accel(12)", "stab_att_ref_rate(16)","stab_att_ref_quat(15)" references défined by two order model | |||
- stabilization_cmd[X] (X=ROLL, PITCH, YAW) commands défined by a feedforward part and feedback part, feedback part is based on PID | |||
- quaternions define the orientation of rotorcraft, | |||
- the error between the quat_sp and the quat_ref is computed by a quaternion product, | |||
- the dot_quaternion is computed by the formula <math>\frac{1}{2} M_s(p,q,r) Q</math> | |||
- The second order model : | |||
-- Integrates accelerate to obtain "stab_att_ref_rate" by the Euler method | |||
-- Integrates rate to obtain "stab_att_ref_quat" by the Euler method | |||
-- The Euler method uses dt. Here dt is implicite and equal 1/512 or <math>2^9</math>, | |||
-- Determines the stab_att_ref_accel(12) by a second order <math>\frac{\Omega^2}{s^2+2 \Zeta \Omega s + \Omega^2}</math> with <math>\Omega = 200*\pi/180</math> and <math>\Zeta = 0.9</math>.<math>\Omega </math> and <math>\Zeta </math> are defined in airframe.xml. | |||
* The second order | |||
[[File:fiche3.jpg]] | |||
* Feedforward part | |||
[[File:fiche4.jpg]] | |||
*Feedback part | |||
[[File:fiche5.jpg]] | |||
* Comments | |||
With the assumption of small variations so <math>sin(\phi) = \phi</math> and so on for pitch and yaw, terms of second order are ignored : | |||
- <math>q_e = 1</math> | |||
- <math>q_x = \psi/2 - \theta/2 * \phi/2 = \psi/2 </math> | |||
- <math>q_y = \theta/2 - \psi/2 *\phi/2 = \theta/2 </math> | |||
- <math>q_z = \phi/2 - \theta/2 * \psi/2 = \phi/2 </math> | |||
Latest revision as of 23:32, 7 August 2013
Control command based of quaternions
Files :
- stabilization_attitude_quat_int.c (.h)
- stabilization_attitude_ref_quat_int.c (.h)
- quat_setpoint_int.c (.h)
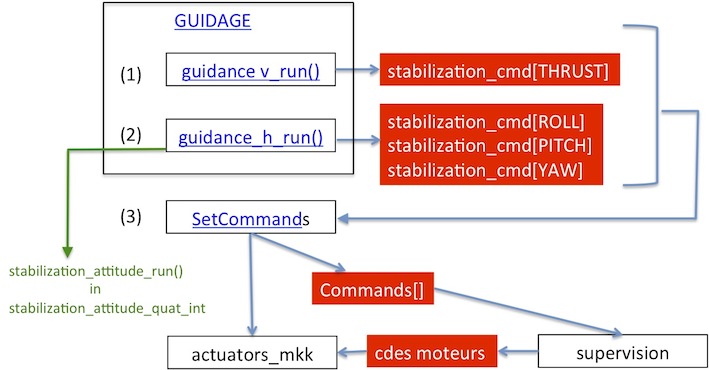
- Position in the autopilot structure
- Control structure
note : () number of decimals for integer calculus
- Comments
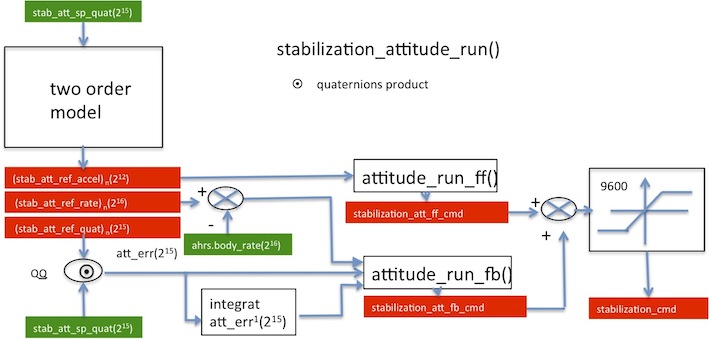
- "stab_att_sp_quat (15)" attitude to reach
- "stab_att_ref_accel(12)", "stab_att_ref_rate(16)","stab_att_ref_quat(15)" references défined by two order model
- stabilization_cmd[X] (X=ROLL, PITCH, YAW) commands défined by a feedforward part and feedback part, feedback part is based on PID
- quaternions define the orientation of rotorcraft,
- the error between the quat_sp and the quat_ref is computed by a quaternion product,
- the dot_quaternion is computed by the formula
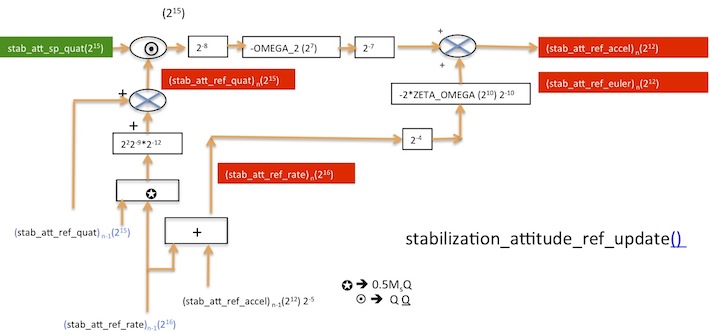
- The second order model :
-- Integrates accelerate to obtain "stab_att_ref_rate" by the Euler method
-- Integrates rate to obtain "stab_att_ref_quat" by the Euler method
-- The Euler method uses dt. Here dt is implicite and equal 1/512 or ,
-- Determines the stab_att_ref_accel(12) by a second order with and . and are defined in airframe.xml.
- The second order
- Feedforward part
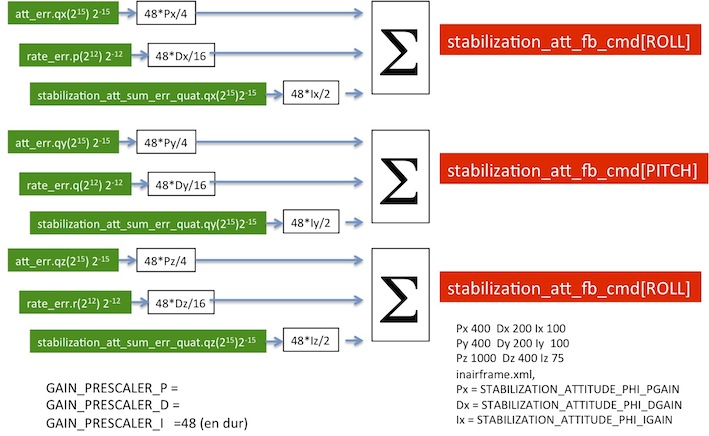
- Feedback part
- Comments
With the assumption of small variations so and so on for pitch and yaw, terms of second order are ignored :
-
-
-
-