User:Jouvencel

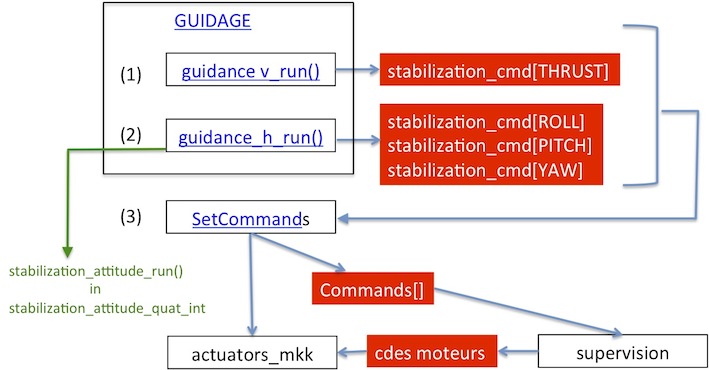
Control command based of quaternions

Files : stabilization_attitude_quat_int.c (.h)

stabilization_attitude_ref_quat_int.c (.h)

quat_setpoint_int.c (.h)

• Position in the autopilot structure

• Control structure

note : ($2^{''N''}$) number of decimals for integer calculus

• Comments

- "stab_att_sp_quat (15)" attitude to reach

- "stab_att_ref_accel(12)", "stab_att_ref_rate(16)","stab_att_ref_quat(15)" references défined by two order model

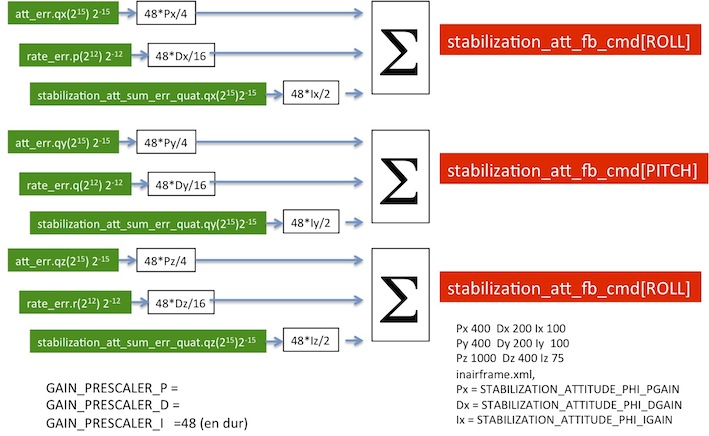
- stabilization_cmd[X] (X=ROLL, PITCH, YAW) commands défined by a feedforward part and feedback part, feedback part is based on PID

- quaternions define the orientation of rotorcraft,

- the error between the quat_sp and the quat_ref is computed by a quaternion product,

- the dot_quaternion is computed by the formula ${\frac {1}{2}}M_{s}(p,q,r)Q$

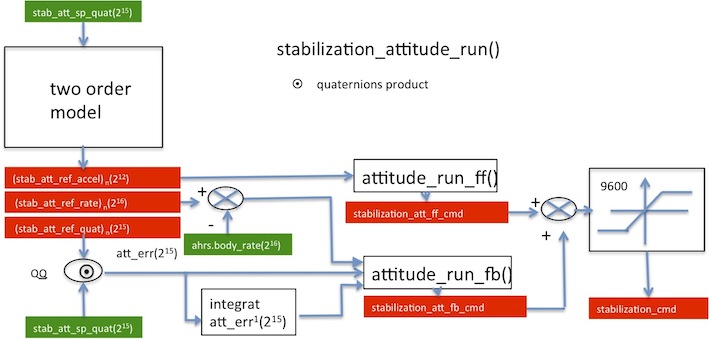
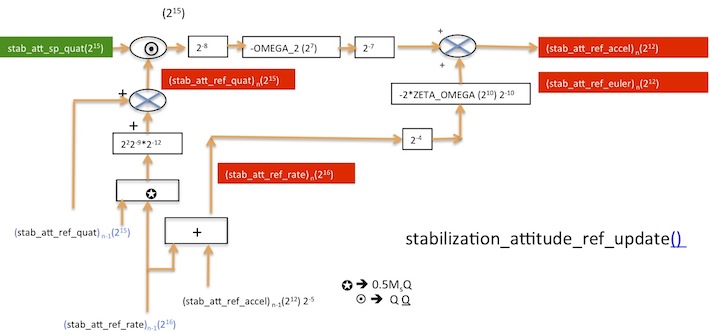
- The second order model :

-- Computes integrated accelerate to obtain "stab_att_ref_rate" by the Euler method

-- Computes integrated rate to obtain "stab_att_ref_quat" by the Euler method

-- The Euler method uses dt here, dt is implicite and equal 1/512 or $2^{9}$,

-- Determines the stab_att_ref_accel(12) by a second order ${\frac {\Omega ^{2}}{s^{2}+2\mathrm {Z} \Omega s+\Omega ^{2}}}$ with $\Omega =200*\pi /180$ and $\mathrm {Z} =0.9$.$\Omega$ and $\mathrm {Z}$ are defined in airframe.xml.

• The second order

• Feedforward part

• Feedback part

• Comments

With the assumption of small variations so $sin(\phi )=\phi$ and so on for pitch and yaw, terms of second order are ignored :

- $q_{e}=1$

- $q_{x}=\psi /2-\theta /2\phi /2=\psi /2$

- $q_{y}=\theta /2-\psi /2\phi /2=\theta /2$

- $q_{z}=\phi /2-\theta /2\psi /2=\phi /2$