Difference between revisions of "Theory of Operation"
| Line 14: | Line 14: | ||
=== Roll Rate === | === Roll Rate === | ||
In <b | {{Box Code|In <b>sw/airborne/fw_h_ctl.c</b> we define the roll rate loop:| | ||
float cmd = throttle_dep_pgain * ( err + h_ctl_roll_rate_igain * roll_rate_sum_err / H_CTL_ROLL_RATE_SUM_NB_SAMPLES + h_ctl_roll_rate_dgain * d_err); | float cmd <nowiki>=</nowiki> throttle_dep_pgain * ( err + h_ctl_roll_rate_igain * roll_rate_sum_err / H_CTL_ROLL_RATE_SUM_NB_SAMPLES + h_ctl_roll_rate_dgain * d_err); | ||
}} | |||
Note that the roll Pgain is variable with throttle and multiplies through the entire equation affecting the I and D terms as well for ease of tuning. | Note that the roll Pgain is variable with throttle and multiplies through the entire equation affecting the I and D terms as well for ease of tuning. | ||
| Line 29: | Line 30: | ||
=== Navigation === | === Navigation === | ||
In <b | {{Box Code|In <b>sw/airborne/fw_h_ctl.c</b> we define the navigation loop:| | ||
float err = estimator_hspeed_dir - h_ctl_course_setpoint; | float err <nowiki>=</nowiki> estimator_hspeed_dir - h_ctl_course_setpoint; | ||
NormRadAngle(err); | NormRadAngle(err); | ||
float speed_depend_nav = estimator_hspeed_mod/NOMINAL_AIRSPEED; | float speed_depend_nav <nowiki>=</nowiki> estimator_hspeed_mod/NOMINAL_AIRSPEED; | ||
Bound(speed_depend_nav, 0.66, 1.5); | Bound(speed_depend_nav, 0.66, 1.5); | ||
float cmd = h_ctl_course_pgain * err * speed_depend_nav; | float cmd <nowiki>=</nowiki> h_ctl_course_pgain * err * speed_depend_nav; | ||
}} | |||
Here we only use the Proportional term though a Derivative would be useful as navigation is not well damped. Note that an Integral term cannot be used for navigtation without accurate and reliable wind information and the necessary implementation of wind data. Note however that we increase/reduce the commanded bank angle for navigation based on the ground speed. This reduces "hunting" on upwind legs, keeps the navigation tight on fast downwind legs and helps keep circles round in a crosswind. | Here we only use the Proportional term though a Derivative would be useful as navigation is not well damped. Note that an Integral term cannot be used for navigtation without accurate and reliable wind information and the necessary implementation of wind data. Note however that we increase/reduce the commanded bank angle for navigation based on the ground speed. This reduces "hunting" on upwind legs, keeps the navigation tight on fast downwind legs and helps keep circles round in a crosswind. | ||
=== Climb Rate === | === Climb Rate === | ||
In <b | {{Box Code|In <b>sw/airborne/fw_v_ctl.c</b> we compute the desired climb rate:| | ||
v_ctl_altitude_error = estimator_z - v_ctl_altitude_setpoint; | v_ctl_altitude_error <nowiki>=</nowiki> estimator_z - v_ctl_altitude_setpoint; | ||
v_ctl_climb_setpoint = v_ctl_altitude_pgain * v_ctl_altitude_error + v_ctl_altitude_pre_climb; | v_ctl_climb_setpoint <nowiki>=</nowiki> v_ctl_altitude_pgain * v_ctl_altitude_error + v_ctl_altitude_pre_climb; | ||
}} | |||
Here we only use the Proportional term though a Derivative would be useful as climb rate is not well damped. An integral term may prove useful if well-implemented. The last term <b><tt>v_ctl_altitude_pre_climb</tt></b> represents the desired constant climb rate needed to follow a 3-dimensional navigation path. This term is zero for level flight, altitude maintenance, and commanded altitude changes. | Here we only use the Proportional term though a Derivative would be useful as climb rate is not well damped. An integral term may prove useful if well-implemented. The last term <b><tt>v_ctl_altitude_pre_climb</tt></b> represents the desired constant climb rate needed to follow a 3-dimensional navigation path. This term is zero for level flight, altitude maintenance, and commanded altitude changes. | ||
{{Box Code|Then we compute the throttle response:| | |||
Then we compute the throttle response: | float err <nowiki>=</nowiki> estimator_z_dot - v_ctl_climb_setpoint; | ||
float err | float controlled_throttle <nowiki>=</nowiki> v_ctl_auto_throttle_cruise_throttle + v_ctl_auto_throttle_climb_throttle_increment * v_ctl_climb_setpoint | ||
float controlled_throttle = v_ctl_auto_throttle_cruise_throttle + v_ctl_auto_throttle_climb_throttle_increment * v_ctl_climb_setpoint | |||
+ v_ctl_auto_throttle_pgain * (err + v_ctl_auto_throttle_igain * v_ctl_auto_throttle_sum_err); | + v_ctl_auto_throttle_pgain * (err + v_ctl_auto_throttle_igain * v_ctl_auto_throttle_sum_err); | ||
and pitch response | and pitch response | ||
float v_ctl_pitch_of_vz = v_ctl_climb_setpoint * v_ctl_auto_throttle_pitch_of_vz_pgain; | float v_ctl_pitch_of_vz <nowiki>=</nowiki> v_ctl_climb_setpoint * v_ctl_auto_throttle_pitch_of_vz_pgain; | ||
}} | |||
== Infrared Sensors == | == Infrared Sensors == | ||
Revision as of 16:14, 30 December 2006
Formal Methods
The critical core of the Paparazzi code has been proven by formal methods to ensure absolute reliability of the servo, R/C, and manual control portions of the code using the same tools and methods used for full-scale autopilots, nuclear power plants, and other critical control systems. See our page on formally proving critical Paparazzi code using Lustre.
PID
Paparazzi uses common Proportional Integral Derivative (PID) control for stability and navigation. PID is probably the most commonly used feedback control design as it is simple to implement and intuitive to operate. PID controllers use three terms operating on the measured error to produce a control output. If u(t) is the control signal sent to the system, y(t) is the measured output and r(t) is the desired output, and tracking error , a PID controller has the general form
The desired closed loop dynamics are obtained by adjusting the three parameters , and , often iteratively by "tuning" and without specific knowledge of a plant model. Stability can often be ensured using only the proportional term in well damped systems. The integral term compensates for steady long-term errors, and the derivative term is used to provide damping to reduce oscillation.
See more on Wikipedia: PID Controller
Paparazzi uses PID controllers on all loops but many of the I and D terms are not fully implemented as they are often unnecessary or difficult to tune. Below are some examples of the PID implementations in Paparazzi.
Roll Rate
| File: In sw/airborne/fw_h_ctl.c we define the roll rate loop: |
float cmd = throttle_dep_pgain * ( err + h_ctl_roll_rate_igain * roll_rate_sum_err / H_CTL_ROLL_RATE_SUM_NB_SAMPLES + h_ctl_roll_rate_dgain * d_err); |
Note that the roll Pgain is variable with throttle and multiplies through the entire equation affecting the I and D terms as well for ease of tuning.
Pitch Angle
| File: In sw/airborne/fw_h_ctl.c we define the pitch angle loop: |
float err = estimator_theta - h_ctl_pitch_setpoint; float d_err = err - last_err; last_err = err; float cmd = h_ctl_pitch_pgain * (err + h_ctl_pitch_dgain * d_err) + h_ctl_elevator_of_roll * fabs(estimator_phi); |
Here we use only Proportional as the Derivative is always set to zero. An integral term could prove useful here. Aircraft pitch response is normally very well damped. Those with "plank" style aircraft or other pitch-sensitive designs may benefit from implementing a gyro-based D term.
| File: In sw/airborne/fw_h_ctl.c we define the navigation loop: |
float err = estimator_hspeed_dir - h_ctl_course_setpoint; NormRadAngle(err); float speed_depend_nav = estimator_hspeed_mod/NOMINAL_AIRSPEED; Bound(speed_depend_nav, 0.66, 1.5); float cmd = h_ctl_course_pgain * err * speed_depend_nav; |
Here we only use the Proportional term though a Derivative would be useful as navigation is not well damped. Note that an Integral term cannot be used for navigtation without accurate and reliable wind information and the necessary implementation of wind data. Note however that we increase/reduce the commanded bank angle for navigation based on the ground speed. This reduces "hunting" on upwind legs, keeps the navigation tight on fast downwind legs and helps keep circles round in a crosswind.
Climb Rate
| File: In sw/airborne/fw_v_ctl.c we compute the desired climb rate: |
v_ctl_altitude_error = estimator_z - v_ctl_altitude_setpoint; v_ctl_climb_setpoint = v_ctl_altitude_pgain * v_ctl_altitude_error + v_ctl_altitude_pre_climb; |
Here we only use the Proportional term though a Derivative would be useful as climb rate is not well damped. An integral term may prove useful if well-implemented. The last term v_ctl_altitude_pre_climb represents the desired constant climb rate needed to follow a 3-dimensional navigation path. This term is zero for level flight, altitude maintenance, and commanded altitude changes.
| File: Then we compute the throttle response: |
float err = estimator_z_dot - v_ctl_climb_setpoint; float controlled_throttle = v_ctl_auto_throttle_cruise_throttle + v_ctl_auto_throttle_climb_throttle_increment * v_ctl_climb_setpoint + v_ctl_auto_throttle_pgain * (err + v_ctl_auto_throttle_igain * v_ctl_auto_throttle_sum_err); and pitch response float v_ctl_pitch_of_vz = v_ctl_climb_setpoint * v_ctl_auto_throttle_pitch_of_vz_pgain; |
Infrared Sensors
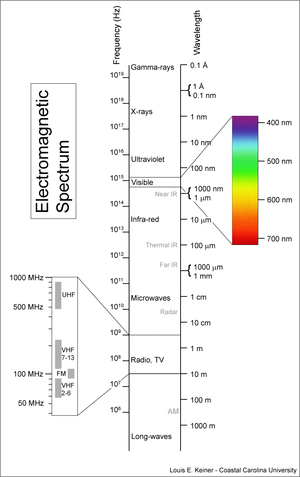
The infrared spectrum spans the gap between red light and microwave radiation and consists of a very large range of wavelengths from 0.75µm to 1000µm (compare to 0.38µm to 0.75µm for the entire range of visible light). With such a broad range, it is not surprising that the properties of IR radiation vary widely with wavelength and therefore are usually categorized as follows:
- near infrared (NIR, IR-A): 0.75–1.4 µm, this range is defined by the water absorption properties and is commonly used in fiber optic communication because of low attenuation losses in the SiO2 glass (silica) fiber.
- short wavelength IR (SWIR, IR-B): 1.4–3 µm, water absorption is substantial in this range.
- mid wavelength IR (MWIR, IR-C) also intermediate-IR (IIR): 3–8 µm
- long wavelength IR (LWIR, IR-C): 8–15 µm (The wavelength used by the Paparazzi IR sensors)
- far infrared (FIR): 15–1,000 µm (FIR lasers are used to detect explosives and chemical agents by infrared spectroscopy)
Near IR behaves much like red light, and can be focused in a glass lens or used to illuminate objects and is commonly used for dramatic effects in photography. Digital cameras are highly sensitive to NIR and typically include a filter to prevent this light from degrading the quality of the visible range.
LWIR is more similar to microwave, and is a form of radiation emitted from within any material of any temperature above absolute zero. The emitted frequency is dependent on the temperature of the material and objects of common "earthly" temperatures typically emit radiation in the range of 8-12µm. The IR sensors used by Paparazzi are sensitive only to this range and therefore are not affected by objects of higher temperature, such as the sun. This range of IR passes easily through smoke and rain but can be blocked with a simple piece of clear tape.
The IR thermopiles used for attitude detection use the thermoelectric effect to convert heat to voltage. They require no power and the voltage produced is extremely low ~ 40µV/K. To convert this low voltage into something that can be measured by the autopilot we first connect the sensors in geometrically opposed pairs and wire them together backwards - output-to-output, such that the system will produce 0V if the sensors are of equal temperature, and any difference between temperatures creates either a positive or negative voltage. Next we amplify this voltage by a factor of 500x and add a 1.65V DC offset. The result is that for normal earthly temperatures, the sensor pair will output a voltage of 0V - 3.3V at extreme temperature differences and 1.65V at equilibrium.
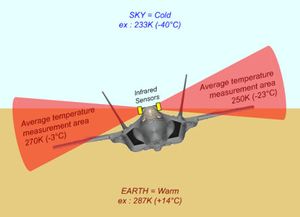
As the Earth emits substantially more IR radiation than the sky, we can always measure the difference between Earth and sky - even in cloudy/rainy weather, over snow covered land, or at night. The voltage produced by the sensor pair is proportional to two factors:
- The angle of the aircraft
- The local ground/sky temperature difference
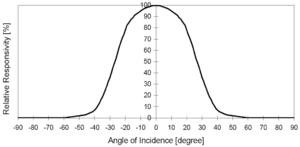
The sensors typically have a 100 degree field of view and produce a somewhat sinusoidal voltage response relative to their angle orientation. as seen in the plot to the right. By combining the data from 3 orthogonal pairs of sensors (X, Y, Z axes) we can compute the exact bank and pitch angles of the aircraft in any weather/terrain conditions with the following caveats:
- Thermopile response is not perfectly sinusoidal so some approximate correction factors must be manually tuned
- Thermopiles react slowly (~25ms time constant), producing a phase delay that can cause oscillation on agile airplanes if a gyro is not implemented
For simple stable aircraft, a 2-axis IR system can be employed by simply measuring the absolute earth/sky temperature difference prior to flight and storing this value. The software has a function to make this easy - when enabled the user simply holds the aircraft nose-down and moves the aileron stick to store the value. This method can produce satisfactory results but will severely reduce navigation consistency as all bank angles will be computed relative to the patch of ground and cloud conditions of the launch site.