Actuator Dynamics
Some stabilization modules require an estimation of the current actuator states. Examples are the INDI and INCA modules. When actuator feedback is not available, this estimation can be mathematical model of the actuators. For brushless motors, a first order transfer function often suffices as actuator model. This guide describes how to accurately determine a first order approximation for a motor with a propeller. Note that the actuator dynamics vary for each configuration of different motors, propellers and ESCs (Electronic Speed Controllers). Used for this example are:
- Cobra C-2814/16 brushless motor, KV=1050
- HQProp 7040 7x4 Propeller Slow Flyer 2 Blade Nylon/Glass Fiber Composite
- KISS ESC 24A re – 32bit Electronic Speed Controller
Actuator model
With this method, actuators are approximated by a first order model in de following form:
where is the actuator transfer function in the Laplace domain, is the system's gain, and is the system's time constant.
When using such a model on discrete time systems, an estimation of an actuator's current position () can be calculated as a function of the current actuator command () and the previous estimation of its position ():
where
where is the duration of one time step
To make a good approximation of actuator dynamics, one needs to determine appropriate values for and
Measuring Actuator Response
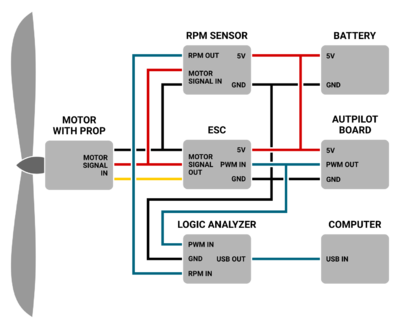
The first step in approximating actuator dynamics is to measure actuator response. This can be done with by connecting an RPM sensor to the motor's wires, and recording both the ESC's input PWM and output RPM signals. An schematic representation of the setup used for this example is shown in the figure below:
Used for the setup of this example:
- Orange RPM Sensor for RPM measurements
- Saleae Logic 8 Digital Analyzer for recording measurements
- MATLAB for analyzing measurements
In order to get a representative model for the whole range of the motor, control the motor with varying speeds and varying step sizes in the PWM signal. You can use Paparazzi's module servo_tester, which runs a predefined program. Try to experiment a bit with the module's settings to create a test program suitable for your purpose, and make sure to firmly attach your motor before running the program.
You can record the PWM and RPM signals with your digital analyzer. Make sure to select appropriate bitrates. Saleae provides a function in their software with which you can export your measurements to a MATLAB file, which you can read with the MATLAB script below.
Data Processing
With the following MATLAB script, you can make the estimation of you first order actuator model's time constant. In the script, indicate the file name of your measurements, the channel numbers for the different types of data, and the timeframe in which you recorded your relevant data. You can also specify different values of tau to try. The script will try these values, and interpolate results to find the tau with which the simulated response best fits the measured response. Don't forget to set the correct frequency at which your module runs if you want to get a correct value for alpha as well. The minimal period settings are used to filter out any signal changes that are too quick, and are therefore probably misreadings.
%{
This script is written for estimation of first order actuator dynamics for
motors with rotors. It uses measurements of both a PWM input signal and the
actuator's RPM response, and tries to fit a first order model to these data
of de form:
K
-----------
tau * s + 1
This form can be used to estimate a actuator's state as a function of its
previous state and its current input as follows:
u_est = u_prev + alpha * (u - u_prev)
where alpha = 1 - e^(tau * dt)
© H.J. Karssies - Delft University of Technology
%}
% Close figures and clear workspace
clc
clear all
close all
% Settings
data_file = 'motor_data_04.mat'; % Data file
pwm.channel_no = 0; % Channel number of PWM input data
pwm.period_min = 0.0005; % Minimum PWM period used for filtering
rpm.channel_no = 1; % Channel number of RPM measurement data
rpm.period_min = 0.00005; % Minimum RPM period used for filtering
t_min = 5; % Starting time of relevant data (s)
t_max = 10.4; % End time of relevant data (s)
taus = 5:5:100; % List of values for tau to try (s)
main_freq = 512; % Paparazzi main frequency
% Load data
raw_data = load(data_file);
pwm = load_channel(pwm, raw_data);
rpm = load_channel(rpm, raw_data);
pwm.freq = length(pwm.time)/(pwm.time(end)-pwm.time(1));
% Calculate motor frequencies
pwm.motor_freq = pwm.period*1000000;
rpm.motor_freq = 1./rpm.period;
% Check performance for different values of tau
for n = 1:length(taus)
errors(n) = calc_performance(taus(n), pwm, rpm, t_min, t_max, false);
end
% Interpolate results and find minimum
taus_int = taus(1):0.01:taus(end);
errors_int = spline(taus, errors, taus_int);
error_min = min(errors_int);
tau_min = taus_int(find(errors_int == error_min));
alpha = 1-exp(-tau_min/main_freq);
% Plot result
figure;
set(gcf, 'Position', [100, 100, 1080, 540]);
subplot(1,2,1);
plot(taus_int, errors_int);
hold on
scatter(tau_min, error_min, 'black');
grid on
title("\tau estimation");
xlabel("\tau (s)");
ylabel("Error (rpm²)");
text(tau_min, error_min+0.1*diff(ylim), ...
[sprintf("\\tau = %.2f s", tau_min); ...
sprintf("\\alpha = %.5f (%d Hz)", [alpha, main_freq])]);
% Perform calculations with final tau and plot figures
calc_performance(tau_min, pwm, rpm, t_min, t_max, true);
% Load channel data and process it
function channel = load_channel(channel, data)
% Process channel
channel_data = eval('data.digital_channel_' + string(channel.channel_no));
channel.bit_1 = data.digital_channel_initial_bitstates(channel.channel_no+1);
channel.period = channel_data(2-channel.bit_1:2:end)./data.digital_sample_rate_hz;
channel.time = cumsum(channel_data./data.digital_sample_rate_hz);
channel.time = channel.time(2-channel.bit_1:2:end);
% Filter out invalid data
channel.time = channel.time(channel.period>channel.period_min);
channel.period = channel.period(channel.period>channel.period_min);
end
% Calculate performance with certain tau
function error = calc_performance(tau, pwm, rpm, t_min, t_max, plot_fig)
% Simulate RPM response
motor = tf(tau,[1 tau]);
% Run simulation at rounded PWM sample times
bias = mean(pwm.motor_freq(1:10));
dt = 1/round(pwm.freq);
t = [0:length(pwm.time)-1]*dt;
motor = tf(tau,[1 tau]);
sim_pwm_freq = lsim(motor, pwm.motor_freq-bias, t) + bias;
% Get the RPM requency values at the rounden PWM sample times
int_rpm_freq = interp1(rpm.time,rpm.motor_freq,t,[],1)';
int_rpm_freq(isinf(int_rpm_freq)) = 1;
% Fit a simple model y = ax + b
data_range = and(t>=t_min, t<=t_max);
inputs = [ones(size(sim_pwm_freq(data_range))) ...
sim_pwm_freq(data_range)];
gain = inputs \ int_rpm_freq(data_range);
sim_rpm_freq = inputs*gain;
% Calculate squared error
error = sum((int_rpm_freq(data_range)-sim_rpm_freq).^2);
% Plot figure
if plot_fig
subplot(1,2,2);
plot(pwm.time, pwm.motor_freq)
hold on
plot(rpm.time, rpm.motor_freq)
plot(pwm.time(data_range), sim_rpm_freq)
grid on
xlim([0, max(pwm.time)]);
ylim([0, 1.2*max(rpm.motor_freq)]);
plot([t_min t_min], ylim, 'black');
plot([t_max t_max], ylim, 'black');
title(sprintf("PWM signal and response for \\tau = %.2f s", tau));
xlabel("Time (s)");
ylabel("Duty time (ms) / motor speed (rpm)");
legend(["PWM signal", "RPM measurement", ...
"Response approximation"])
end
end